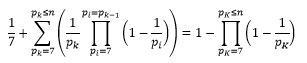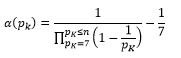Eis a igualdade mais inútil que eu já obtive para o estudo de sucessões

E podemos definir a sucessão alfa relativa à sucessão u como sendo

Como se distribuem os números primos entre os números naturais

Dizer que entre os valores Un=30n+1 e Vn=30n+29, para um determinada ordem n existem no máximo 8 números primos demonstra-se de:

1) a união das sucessões Un=30n-29 e Vn=30n-19 contém todos os números primos terminados em 1
2) a união das sucessões Un=30n-17 e Vn=30n-7 contém todos os números primos terminados em 3 com excepção do número primo 3
3) a união das sucessões Un=30n-23 e Vn=30n-13 contém todos os números primos terminados em 7
4) a união das sucessões Un=30n-11 e Vn=30n-1 contém todos os números primos terminados em 9
5) os números primos 2, 3 e 5 são números menores que 31 ou seja números minorantes da sucessão Un=30n+1

Mas as sucessões Un=30n-29, Un=30n-23, Un=30n-19, Un=30n-17, Un=30n-13, Un=30m-11, Un=30n-7 e Un=30n-1,
contém a partir da ordem de um número resultante da sucessão p,
ou da ordem de um número resultante da sucessão que seja um número múltiplo de p,
de p em p elementos de ordem da sucessão,
um número resultante da sucessão que é um número múltiplo de p.

Cada uma das 8 sucessões contém múltiplos de 7, de 7 em 7 elementos da sucessão e

para a sucessão Un=30n-11 o conjunto de múltiplos de 7 é dado por n pertencente a { 2,  9, 16, ...} ou seja n=7m-5

para a sucessão Un=30n-13 o conjunto de múltiplos de 7 é dado por n pertencente a { 3, 10, 17, ...} ou seja n=7m-4

para a sucessão Un=30n-29 o conjunto de múltiplos de 7 é dado por n pertencente a { 4, 11, 18, ...} ou seja n=7m-3

para a sucessão Un=30n-17 o conjunto de múltiplos de 7 é dado por n pertencente a { 5, 12, 19, ...} ou seja n=7m-2

para a sucessão Un=30n-19 o conjunto de múltiplos de 7 é dado por n pertencente a { 6, 13, 20, ...} ou seja n=7m-1

para a sucessão Un=30n-7  o conjunto de múltiplos de 7 é dado por n pertencente a { 7, 14, 21, ...} ou seja n=7m

para a sucessão Un=30n-23 o conjunto de múltiplos de 7 é dado por n pertencente a { 8, 15, 22, ...} ou seja n=7m+1

Porque para n=1 o conjunto contém o número 1 que não é um número primo,

podemos concluir que para qualquer n>1 um dos elementos de uma das sucessões acima é obrigatoriamente um número múltiplo de 7

Fica então demonstrado que entre os valores Un=30n+1 e Vn=30n+30,

para qualquer número de ordem n que seja determinado, existem no máximo 7 números primos.

Ou seja, que com excepção dos primeiros 30 números naturais [1, 30], 

todos os outros grupos de trinta números naturais subsequentes,

definidos por [30n, 30n+30], contém no máximo 7 números primos.

Ou seja a quantidade dos primos p em relação à quantidade de números naturais n, 

é inferior a 7 números primos por cada 30 números naturais 

ou seja a cardinalidade dos números naturais sobre a cardinalidade dos números primos é

estritamente superior a 30/7 ou seja superior a 4,(285714) números naturais por cada número primo.

A partir do estudo dos números múltiplos dos números primos existentes na sucessão u_n=2x3x5n-29, deduz-se que a probabilidade de um número natural n ser primo pode ser dada por

Que tende por hipótese  para zero, quando n tende para infinito e então

Como

fazendo

Podemos reescrever o multiplicatório relacionando-o com esta sucessão que é uma função de pk e reescrever o somatório do múltiplicatório na forma

E de 1/7+(1-1/7)/11+(1-1/7)(1-1/11)/13+(1-1/7)(1-1/11)(1-1/13)/17+…=1

A probabilidade de um número natural maior ou igual a 7 ser um número primo vém então aproximadamente igual a 

E resolvendo o somatório em função de alfa obtemos

E considerando pk≥7 podemos ajustar α(pk) a uma sucessão aproximada do tipo

Em que a1≈0,00025, a2≈0,99877, a3≈0,00127,  a4≈0,448154823950443 e a5≈0,82772

Como todos os parâmetros acima afectam alfa linearmente, podemos fixar 4 e aproximar alfa pela variação de apenas um dos parâmetros.

Assim escolhemos para este efeito o parâmetro a4.

Podemos ainda escrever alfa na forma

Em que x é a  maior solução de entre as duas soluções da seguinte função quadrática

A aproximação da sucessão acima à sucessão real de alfa verifica a inequação abaixo

Ou seja