Números Primos

Breve estudo dos números primos

Aproximação aos números primos

Obtendo para quantidades variáveis de números primos uma aproximação a uma expressão polinomial do quarto grau do tipo

para os elementos ordenados do conjunto dos primos que denominaremos por  

e analisando a variação dos coeficientes obtidos como sendo funções de potências para a₁, a₂, a₃

e uma função logarítmica para o parâmetro linear no formato  

e considerando o último coeficiente na forma

obtemos as seguintes funções 

As quais podemos aproximar à função linear acima apresentada.

Subtraindo aos primos  os valores desta função e dividindo por x e aproximando os valores resultantes à função logarítmica no formato

Obtemos

Basta agora voltar a multiplicar por x e somar a função linear anteriormente obtida e obtemos a função com o menor número de parâmetros e com o menor desvio para esta quantidade de parâmetros que se aproxima de todos os números primos como sendo

O gráfico da diferença  entre os valores desta função e o correspondente número primo é uma função aleatória como se ilustra 

E se  pretendermos estudar, como realmente pretendíamos, estes desvios dos números primos a esta função,  temos uma tarefa impossível, porque somos confrontados com uma variável aleatória.

Abordagem periódica à análise dos números primos 

Se fizermos o cosseno dos valores da sucessão de números primos o gráfico que se nos apresenta é o que se ilustra abaixo e ele já não parece tão aleatório

É fácil verificar que o período destas 23 sub-sucessões de cossenos ao redor das quais se distribuem os números primos é de  

Os valores iniciais a atribuir a cada uma destas sub-sucessões do tipo 

são dados por





e podem ser calculado a partir dos pontos dos gráficos que se apresentam abaixo,  que são a resultante

das sub-sucessões obtidas por

que denominei de sub-sucessões resolventes dos números primos

A  melhor aproximação que obtive para o valor inicial é a=-844,375228726084

Esta tabela é o resultado parcial da distribuição dos primos por aproximação às sub-sucessões anteriores 

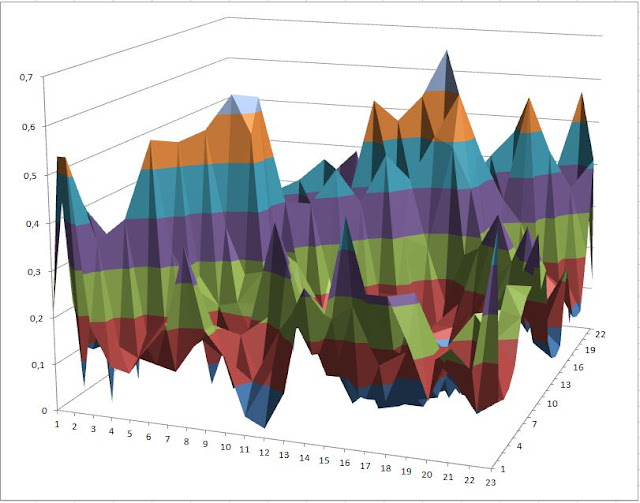
A distribuição dos números primos por estas 23 sub-sucessões tem o gráfico de probabilidades que se segue para os primeiros 10000 primos

Se o gráfico de distribuição dos números primos por estas 23 sub-sucessões será ou parece vir a ser um gráfico uniformemente distribuído em torno do valor 4,34782608695652 como se espera de uma variável aleatória, já o gráfico de probabilidade do valor primo seguinte se encontrar  numa das 23 sub-sucessões definidas não tem nada de uniforme como se pode constatar, o que serve para demonstrar que existe um condicionamento entre o valor de um primo e o valor que pode tomar o primo seguinte de acordo com o quadro seguinte e os gráficos que o representam

Gráfico que na vista de topo permite perceber a verdadeira dimensão da relação entre um número primo e o número primo seguinte

O gráfico acima mostra que existe uma forte tendência para que a os números primos consecutivos se  encontrarem em sub-sucessões consecutivas privilegiando um dos sentidos, ou o  ascendente ou o descendente.

A análise de todos os resultados de arccos(cos(primos)) permite o seguinte desenvolvimento

Não sendo condição suficiente é condição necessária para que um número seja primo, com a excepção do número primo 2, que verifique uma de quatro equações de identidade abaixo escritas

Comecemos por definir um conjunto de variáveis auxiliares

As expressões de identidade das quais é necessário cumprir uma para que um número possa ser primo podem ser escritas então como

Um número que seja um número primo tem ainda de verificar a condição

Sabemos ainda que um número primo, com as excepções  dos números primos 2 e 3, tem também de verificar um dos módulos seguintes

Podemos ainda excluir dos números primos todos os números que são divisíveis por 3 com excepção do próprio 3

Apresentamos um quadro com alguns valores das distribuições dos primos para uma parte da primeira condição

Os números que verificam as duas condições de identidade resultantes  b1(8,±a) são todos múltiplos de 71.

O número primo 71 encontra-se solitário na condição b3(22,+a) e a condição b3(22,-a) não contém primos tal como não os contém as condições b1(8,±a).

Apresento a lista ordenada de todos os valores para o primeiro primo  existente em b1, b3, b7 e b9 para todos os n e para ±a

p1(k,b3(27,+a))=p1(k,461)

p2(k,b1(23,+a))=p2(k,1667)

p3(k,b7(26,-a))=p3(k,1091)

p4(k,b3(11,+a))=p4(k,491)

p5(k,b1(2,-a))=p5(k,113)

p6(k,b3(23,-a))=p1(k,419)

p7(k,b9(2,+a))=p7(k,773)

p8(k,b1(24,-a))=p8(k,953)

p9(k,b1(10,+a))=p9(k,227)

p10(k,b3(6,-a))=p10(k,1319)

p11(k,b9(4,+a))=p11(k,503)

p12(k,b7(14,+a))=p12(k,1949)

p13(k,b7(20,-a))=p13(k,281)

p14(k,b1(13,-a))=p14(k,2663)

p15(k,b9(9,+a))=p15(k,3023)

p16(k,b7(1,-a))=p16(k,911)

p17(k,b9(33,-a))=p17(k,1637)

p18(k,b1(25,-a))=p18(k,23)

p19(k,b3(34,-a))=p19(k,839)

p20(k,b1(27,+a))=p20(k,3257)

p21(k,b1(16,-a))=p21(k,2003)

p22(k,b3(36,+a))=p22(k,311)

p23(k,b3(13,+a))=p23(k,2351)

p24(k,b1(12,+a))=p24(k,2087)

p25(k,b1(18,+a))=p25(k,1277)

p26(k,b3(32,-a))=p26(k,569)

p27(k,b9(14,+a))=p27(k,1283)

p28(k,b9(34,-a))=p28(k,2837)

p29(k,b9(30,-a))=p29(k,167)

p30(k,b1(26,+a))=p30(k,197)

p31(k,b1(13,+a))=p31(k,887)

p32(k,b1(15,+a))=p32(k,617)

p33(k,b9(16,+a))=p33(k,1013)

p34(k,b9(18,+a))=p34(k,743)

p35(k,b3(4,-a))=p35(k,1049)

p36(k,b3(25,+a))=p36(k,2861)

p37(k,b7(31,+a))=p37(k,719)

p38(k,b1(29,+a))=p38(k,857)

p39(k,b9(27,+a))=p39(k,593)

p40(k,b9(7,+a))=p40(k,1163)

p41(k,b9(21,-a))=p41(k,17)

p42(k,b3(17,+a))=p42(k,1811)

p43(k,b9(32,+a))=p43(k,983)

p44(k,b1(6,+a))=p44(k,2897)

p45(k,b7(6,-a))=p45(k,521)

p46(k,b9(1,+a))=p46(k,1973)

p47(k,b7(11,+a))=p47(k,1289)

p48(k,b1(35,+a))=p48(k,47)

p49(k,b1(36,-a))=p49(k,443)

p50(k,b7(24,-a))=p50(k,821)

p51(k,b1(34,+a))=p51(k,5507)

p52(k,b3(28,-a))=p52(k,29)

p53(k,b3(21,-a))=p53(k,149)

p54(k,b9(11,+a))=p54(k,2753)

p55(k,b9(7,-a))=p55(k,257)

p56(k,b9(15,-a))=p56(k,3467)

p57(k,b3(9,+a))=p57(k,761)

p58(k,b3(33,+a))=p58(k,3911)

p59(k,b1(26,-a))=p59(k,1223)

p60(k,b1(4,-a))=p60(k,383)

p61(k,b1(31,+a))=p61(k,587)

p62(k,b3(3,-a))=p62(k,1979)

p63(k,b3(5,+a))=p63(k,1301)

p64(k,b3(14,+a))=p64(k,1151)

p65(k,b3(35,+a))=p65(k,1511)

p66(k,b7(34,-a))=p66(k,41)

p67(k,b9(13,+a))=p67(k,353)

p68(k,b1(2,+a))=p68(k,1307)

p69(k,b1(35,-a))=p69(k,1373)

p70(k,b7(28,+a))=p70(k,59)

p71(k,b1(34,-a))=p71(k,173)

p72(k,b9(3,-a))=p72(k,1847)

p73(k,b3(6,+a))=p73(k,101)

p74(k,b7(10,+a))=p74(k,359)

p75(k,b9(20,-a))=p1(k,947)

p76(k,b3(7,+a))=p76(k,1031)

p77(k,b1(20,+a))=p77(k,3137)

p78(k,b7(15,-a))=p78(k,1381)

p79(k,b9(20,+a))=p79(k,3313)

p80(k,b1(4,+a))=p80(k,1747)

p81(k,b7(5,-a))=p81(k,31)

p82(k,b9(12,-a))=p1(k,577)

p83(k,b1(20,-a))=p83(k,1123)

p84(k,b1(9,+a))=p84(k,7)

p85(k,b1(19,+a))=p85(k,787)

p86(k,b1(28,-a))=p86(k,73)

p87(k,b3(15,+a))=p87(k,661)

p88(k,b3(3,+a))=p88(k,151)

p89(k,b3(25,-a))=p89(k,1399)

p90(k,b7(19,+a))=p90(k,919)

p91(k,b1(5,-a))=p91(k,163)

p92(k,b7(14,-a))=p92(k,181)

p93(k,b9(5,+a))=p93(k,13)

p94(k,b9(21,+a))=p94(k,2113)

p95(k,b7(22,+a))=p95(k,1579)

p96(k,b7(26,+a))=p1(k,1039)

p97(k,b3(35,-a))=p97(k,619)

p98(k,b9(32,-a))=p98(k,5407)

p99(k,b7(9,+a))=p99(k,139)

p100(k,b1(31,-a))=p1(k,1543)

p101(k,b3(20,-a))=p1(k,1789)

p102(k,b9(19,+a))=p102(k,2383)

p103(k,b9(35,-a))=p103(k,487)

p104(k,b3(28,+a))=p104(k,4231)

p105(k,b9(34,+a))=p1(k,3)

p106(k,b3(18,+a))=p1(k,1321)

p107(k,b3(12,-a))=p107(k,709)

p108(k,b3(2,-a))=p1(k,1489)

p109(k,b3(30,+a))=p1(k,1831)

p110(k,b7(2,-a))=p110(k,691)

p111(k,b9(24,-a))=p1(k,67)

p112(k,b1(17,-a))=p112(k,1783)

p113(k,b7(35,-a))=p1(k,1951)

p114(k,b9(28,-a))=p114(k,607)

p115(k,b7(27,-a))=p1(k,3001)

p116(k,b1(30,+a))=p116(k,367)

p117(k,b9(9,-a))=p117(k,1237)

p118(k,b1(3,-a))=p118(k,4153)

p119(k,b3(19,-a))=p119(k,2719)

p120(k,b3(19,+a))=p120(k,2251)

p121(k,b1(14,-a))=p121(k,313)

p122(k,b7(8,+a))=p122(k,3469)

p123(k,b9(23,-a))=p123(k,997)

p124(k,b7(15,+a))=p124(k,1459)

p125(k,b9(19,-a))=p125(k,457)

p126(k,b9(28,+a))=p126(k,103)

p127(k,b9(24,+a))=p127(k,643)

p128(k,b1(18,-a))=p128(k,853)

p129(k,b3(31,-a))=p129(k,79)

p130(k,b7(19,-a))=p130(k,4051)

p131(k,b7(4,+a))=p1(k,1879)

p132(k,b3(27,-a))=p1(k,1669)

p133(k,b7(21,-a))=p133(k,61)

p134(k,b3(34,+a))=p134(k,1291)

p135(k,b3(21,+a))=p135(k,4111)

p136(k,b3(24,-a))=p1(k,199)

p137(k,b1(9,-a))=p137(k,2833)

p138(k,b7(8,-a))=p138(k,3631)

p139(k,b7(29,+a))=p1(k,1699)

p140(k,b7(2,+a))=p140(k,19)

p141(k,b1(7,+a))=p1(k,277)

p142(k,b1(21,-a))=p142(k,193)

p143(k,b7(7,-a))=p143(k,1721)

p144(k,b7(27,+a))=p144(k,1259)

p145(k,b9(22,-a))=p145(k,1217)

p146(k,b3(9,-a))=p146(k,659)

p147(k,b7(18,-a))=p147(k,11)

p148(k,b7(17,+a))=p148(k,479)

p149(k,b7(12,-a))=p149(k,3461)

p150(k,b3(14,-a))=p150(k,269)

p151(k,b7(35,+a))=p151(k,179)

p152(k,b1(17,+a))=p152(k,347)

p153(k,b9(23,+a))=p153(k,5393)

p154(k,b9(11,-a))=p154(k,797)

p155(k,b1(25,+a))=p1(k,3527)

p156(k,b7(28,-a))=p156(k,1361)

p157(k,b3(26,-a))=p157(k,1889)

p158(k,b1(23,-a))=p158(k,463)

p159(k,b3(8,+a))=p1(k,541)

p160(k,b1(1,+a))=p160(k,1087)

p161(k,b7(16,+a))=p161(k,2389)

p162(k,b9(26,+a))=p162(k,373)

p163(k,b3(17,-a))=p163(k,6709)

p164(k,b7(25,+a))=p164(k,109)

p165(k,b7(30,-a))=p165(k,211)

p166(k,b9(29,+a))=p166(k,1033)

p167(k,b7(34,+a))=p167(k,2089)

p168(k,b1(11,-a))=p168(k,263)

p169(k,b9(25,-a))=p169(k,557)

p170(k,b7(16,-a))=p170(k,1871)

p171(k,b7(5,+a))=p171(k,2099)

p172(k,b9(14,-a))=p172(k,137)

p173(k,b7(18,+a))=p173(k,1409)

p174(k,b9(13,-a))=p174(k,1777)

p175(k,b9(10,-a))=p1(k,307)

p176(k,b3(32,+a))=p176(k,3691)

p177(k,b9(8,+a))=p177(k,673)

p178(k,b1(30,-a))=p1(k,2473)

p179(k,b7(25,-a))=p179(k,601)

p180(k,b9(27,-a))=p180(k,827)

p181(k,b7(6,+a))=p1(k,1609)

p182(k,b9(26,-a))=p182(k,337)

p183(k,b1(10,-a))=p183(k,1193)

p184(k,b7(20,+a))=p184(k,5399)

p185(k,b3(29,-a))=p1(k,1229)

p186(k,b1(3,+a))=p186(k,107)

p187(k,b7(33,+a))=p187(k,449)

p188(k,b7(24,+a))=p188(k,599)

p189(k,b3(8,-a))=p189(k,3719)

p190(k,b3(16,+a))=p190(k,881)

p191(k,b3(18,-a))=p191(k,809)

p192(k,b3(1,+a))=p192(k,421)

p193(k,b7(7,+a))=p193(k,409)

p194(k,b7(10,-a))=p194(k,1061)

p195(k,b3(12,+a))=p195(k,2131)

p196(k,b9(1,-a))=p196(k,157)

p197(k,b7(13,-a))=p197(k,401)

p198(k,b7(22,-a))=p198(k,3391)

p199(k,b9(15,+a))=p199(k,83)

p200(k,b1(33,+a))=p200(k,317)

p201(k,b9(22,+a))=p201(k,2333)

p202(k,b7(4,-a))=p202(k,251)

p203(k,b1(27,-a))=p203(k,293)

p204(k,b3(20,+a))=p204(k,1051)

p205(k,b1(5,+a))=p205(k,547)

p206(k,b3(26,+a))=p206(k,241)

p207(k,b1(29,-a))=p207(k,563)

p208(k,b9(2,-a))=p208(k,647)

p209(k,b7(11,-a))=p209(k,131)

p210(k,b9(17,-a))=p210(k,1607)

p211(k,b7(21,+a))=p211(k,2069)

p212(k,b9(18,-a))=p212(k,677)

p213(k,b7(3,-a))=p213(k,1181)

p214(k,b3(7,-a))=p214(k,389)

p215(k,b7(29,-a))=p215(k,431)

p216(k,b3(23,+a))=p216(k,5261)

p217(k,b3(11,-a))=p217(k,929)

p218(k,b1(24,+a))=p218(k,467)

p219(k,b3(4,+a))=p219(k,6761)

p220(k,b9(10,+a))=p220(k,1823)

p221(k,b1(33,-a))=p221(k,1103)

p222(k,b3(1,-a))=p222(k,1709)

p223(k,b7(3,+a))=p223(k,239)

p224(k,b9(6,-a))=p1(k,1187)

p225(k,b7(31,-a))=p225(k,701)

p226(k,b1(28,+a))=p226(k,2767)

p227(k,b9(17,+a))=p227(k,523)

p228(k,b7(23,-a))=p228(k,331)

p229(k,b9(30,+a))=p229(k,4093)

p230(k,b1(21,+a))=p230(k,2647)

p231(k,b1(14,+a))=p231(k,397)

p232(k,b7(30,+a))=p232(k,499)

p233(k,b7(23,+a))=p233(k,379)

p234(k,b1(16,+a))=p234(k,127)

p235(k,b1(11,+a))=p235(k,1867)

p236(k,b1(15,-a))=p236(k,3643)

p237(k,b1(1,-a))=p237(k,1753)

p238(k,b9(3,+a))=p238(k,283)

p239(k,b3(16,-a))=p239(k,1249)

p240(k,b7(32,+a))=p240(k,229)

p241(k,b3(10,+a))=p241(k,271)

p242(k,b3(10,-a))=p242(k,439)

p243(k,b1(12,-a))=p243(k,43)

p244(k,b9(33,+a))=p244(k,1913)

p245(k,b7(12,+a))=p245(k,89)

p246(k,b1(22,-a))=p246(k,683)

p247(k,b9(8,-a))=p247(k,37)

p248(k,b9(35,+a))=p248(k,223)

p249(k,b3(13,-a))=p249(k,3329)

p250(k,b7(9,-a))=p250(k,571)

p251(k,b3(29,+a))=p251(k,191)

p252(k,b9(6,+a))=p252(k,233)

p253(k,b1(32,+a))=p253(k,97)

p254(k,b7(33,-a))=p254(k,971)

p255(k,b7(13,+a))=p255(k,1019)

p256(k,b1(36,+a))=p256(k,977)

p257(k,b9(12,+a))=p257(k,1553)

p258(k,b1(6,-a))=p258(k,653)

p259(k,b9(31,-a))=p259(k,1367)

p260(k,b3(36,-a))=p1(k,1109)

p261(k,b7(32,-a))=p261(k,1901)

p262(k,b7(1,+a))=p262(k,509)

p263(k,b9(29,-a))=p263(k,1097)

p264(k,b9(31,+a))=p264(k,53)

p265(k,b9(4,-a))=p265(k,1627)

p266(k,b1(7,-a))=p266(k,433)

p267(k,b1(22,+a))=p267(k,1447)

p268(k,b3(30,-a))=p268(k,1009)

p269(k,b3(31,+a))=p269(k,631)

p270(k,b3(33,-a))=p270(k,349)

p271(k,b9(25,+a))=p271(k,863)

p272(k,b7(17,-a))=p272(k,941)

p273(k,b3(5,-a))=p273(k,829)

p274(k,b9(16,-a))=p274(k,1117)

p275(k,b1(19,-a))=p275(k,2053)

p276(k,b3(2,+a))=p276(k,641)

p277(k,b1(32,-a))=p1(k,613)

p278(k,b9(5,-a))=p278(k,4957)

p279(k,b3(24,+a))=p279(k,1931)

p280(k,b3(15,-a))=p280(k,2179)

p281(k,b3(22,+a))=p281(k,71)

p282(k,b3(22,-a))=p282(k,0)

p283(k,b1(8,-a))=p283(k,0)

p284(k,b1(8,+a))=p284(k,0)

Fazendo o gráfico dos k dos 10000 primeiros primos que verificam as condições acima, ordenando as condições pelas curvas logarítmicas do tipo 

que representam a variação dos k para os primos de cada condição obtemos o gráfico seguinte.

Se este padrão for definido, e não tiver nenhum factor aleatório,  e puder ser produzido, e estendido ao infinito, por um algoritmo que não o processo de apuramento pelo conhecimento dos 10000 primeiros primos que o produziu, pudemos afirmar que é possível determinar à priori todos os números primos.

Isolando o padrão dos k correspondentes aos números primos para as primeiras catorze condições ordenadas obtemos um quadro nada promissor de uma solução porque à primeira vista voltamos a ter um padrão verdadeiramente aleatório.

Coisas que por enquanto só eu sei

Se ao adicionarmos a um número primo 710 o resultado for um número primo, então a soma de 710 a esse número primo nunca resulta num número primo.

Existem infinitos pares de primos equidistantes entre si pelo valor de 710, mas não existe nenhum trio de números primos separados entre si  pelo valor de 710.

Só existe um quinteto de números primos equidistantes entre si de 6, que contém os dois únicos quartetos existentes equidistantes entre si de 6, que é o quinteto formado pelos números primos  

5, 11, 17, 23 e 29. 

Sabemos que os valores inteiros das semi-rectas definidas por b=número primo e m=2130, com a excepção dos valores inteiros das semi-recta 

p=71+2130k e p=5+2130k, p=3+2130k e p=2+2130k, 

que só contém respectivamente apenas o número primo 71, o número primo 5, o número primo 3 e o número primo 2, todas as outras contém infinitos números primos.

Sabemos ainda que compilando todas as semi-rectas distinctas que começam pelos 564 números primos da lista abaixo, 564=280x2+4, isto se incluirmos as semi-rectas 

p(k)=71+2130k, p(k)=5+2130k, p(k)=3+2130k e p(k)=2+2130k , 

o conjunto de todas estas semi-rectas contém todos os infinitos números primos que existem.

Pi ∈ {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109, 113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233, 239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,337,347,349,353,359,367, 373,379,383,389,397,401,409,419,421,431,433,439,443,449,457,461,463,467,479,487,491,499, 503,509,521,523,541,547,557,563,569,571,577,587,593,599,601,607,613,617,619,631,641,643,647, 653,659,661,673,677,683,691,701,709,719,727,733,739,743,751,757,761,769,773,787,797,809, 811,821,823,827,829,839,853,857,859,863,877,881,883,887,907,911,919,929,937,941,947,953, 967,971,977,983,991,997,1009,1013,1019,1021,1031,1033,1039,1049,1051,1061,1063,1069, 1087,1091,1093,1097,1103,1109,1117,1123,1129,1151,1153,1163,1171,1181,1187,1193,1201, 1213,1217,1223,1229,1231,1237,1249,1259,1277,1279,1283,1289,1291,1297,1301,1303,1307, 1319,1321,1327,1361,1367,1373,1381,1399,1409,1423,1427,1429,1433,1439,1447,1451,1453, 1459,1471,1481,1483,1487,1489,1493,1499,1511,1523,1531,1543,1549,1553,1559,1567,1571, 1579,1583,1597,1601,1607,1609,1613,1619,1621,1627,1637,1657,1663,1667,1669,1693,1697, 1699,1709,1721,1723,1733,1741,1747,1753,1759,1777,1783,1787,1789,1801,1811,1823,1831, 1847,1861,1867,1871,1873,1877,1879,1889,1901,1907,1913,1931,1933,1949,1951,1973,1979, 1987,1993,1997,1999,2003,2011,2017,2027,2029,2039,2053,2063,2069,2081,2083,2087,2089, 2099,2111,2113,2129,2131,2179,2207,2221,2251,2273,2333,2339,2347,2351,2377,2383,2389, 2417,2459,2473,2521,2543,2557,2647,2657,2659,2663,2683,2689,2711,2713,2719,2741,2753, 2767,2797,2801,2819,2833,2837,2843,2851,2861,2879,2897,2909,2963,2971,2999,3001,3019, 3023,3061,3079,3089,3109,3119,3137,3167,3187,3203,3209,3229,3251,3257,3271,3299,3307, 3313,3319,3329,3371,3373,3391,3461,3463,3467,3469,3499,3517,3527,3533,3541,3547,3571, 3593,3607,3631,3637,3643,3659,3671,3677,3691,3719,3733,3761,3769,3779,3803,3821,3833, 3847,3881,3911,3923,3929,3943,3947,3967,3989,4013,4021,4027,4049,4051,4057,4073,4091, 4093,4099,4111,4139,4153,4177,4201,4231,4253,4421,4447,4549,4561,4583,4621,4637,4663, 4729,4733,4799,4889,4909,4957,5023,5051,5059,5077,5107,5233,5261,5303,5393,5399,5407, 5417,5419,5471,5479,5507,5527,5531,5569,5573,5623,5639,5651,5653,5717,5779,5851,5903, 5939,5987,6029,6067,6079,6089,6101,6113,6163,6197,6199,6217,6301,6311,6317,6337,6353, 6367,6379,6689,6709,6761,6827,6841,6871,6883,7069,7127,7193,7307,7333,7351,7393,7417, 7457,7643,7741,7907,7927,7963,8101,8147,8161,8233,8423,8689,8861,9371,9419,9421,9433, 9601,9631,9941,10181,10259,10369,10429,10487,11057,11161,11443,11923,12007,12119, 12227,12301,12379,12413,12641,12671,12899,13331, 14461,14897,16253,20857,21433}

A vantagem de usarmos estas rectas para uma primeira validação se um número é primo ou não, é a de que normalmente procuraríamos os primos em todos os ímpares que não terminassem em 5 ou seja números a uma distância média entre eles de 2,5 e com estas rectas procuramos os números primos a uma distância média de 3,8035… ou seja temos um ganho automático de  152,1425…%

Outro olhar sobre os números primos

Pode-se ver no gráfico seguinte de 

255 vezes arccos(cosseno(da 2ª diferença finita dos números primos)) 

que estas andam ao redor de apenas 12 valores que tem diferentes probabilidades de ocorrência e que eventualmente no infinito terão valores que irão preencher de forma homogénea  e com igual probabilidade todos os valores possíveis do contradomínio ou seja de 0 a 255π

Considerando que cos(x)=cos(-x) e verificando a sequência das ocorrências destes valores apresentadas no gráfico seguinte

E fazendo a relação entre cada valor e o valor seguinte como se ilustra no gráfico seguinte

A variável de ocorrências de uma função após a ocorrência de qualquer outra ou da própria seria uma variável aleatória pura se o gráfico acima fosse plano, ora a ocorrência de valores tão diferenciados não fornece probabilidades iguais para a ocorrência de qualquer uma das funções restantes ou da própria, ou seja existe um condicionamento oculto a esta variável que lhe retira o estatuto de variável aleatória pura


Esta abordagem de análise dos números primos revela uma ordem insuspeita dos mesmos e deve ser a única via viável de análise dos mesmos